考试周除了学习什么都好玩,偶然发现了B站上的“精翻”视频,就冲了
第一章的视频还没看完(太长了quq),这里也只是写了整形的lab,写了大概有一整天
明天烤完高代就滚回来填这个lab、课程笔记、导论4、集合论习题的坑...好像有点多,不管了
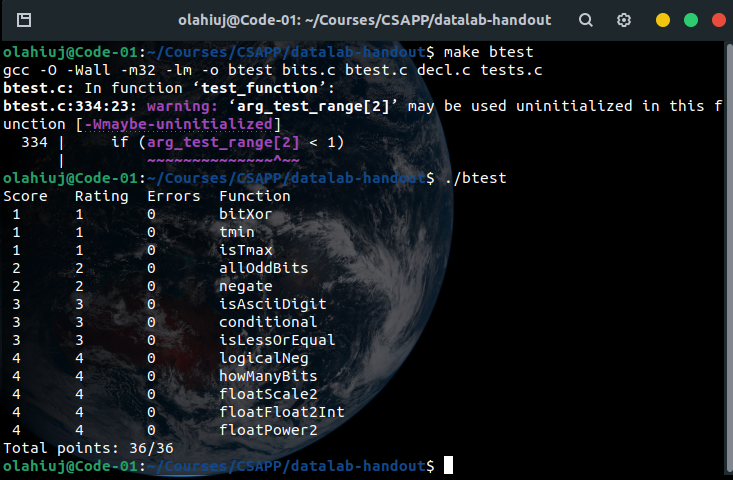
这些只在本地btest过,不保证能对...如果有错或者有更好的做法欢迎指正!
upd:做完了,爽耶
tricks
- \([a=b]\iff [(a \otimes b)=0]\iff [(a-b)=0]\)
这个视能否使用"-"和"^"来选择,相当于不用if做出了判断是否相等
\((111\dots 11)_2=(-1)_{10}\) 这个...没啥好说的
\(f(flag,x)=\left\{ {\begin{aligned}0,flag=0\\x,flag=1\end{aligned} }\right.\iff x\&(-flag)\),结合2就可以理解,结合4很有用
\((-x)=( (\sim x) + 1)\),这个实际上就是电路中减法的做法,这里可以看出反码在简化运算中的作用
bitXor
根据集合论/数理逻辑的知识可以很快想到异或的"对称差"定义
//1
/*
* bitXor - x^y using only ~ and &
* Example: bitXor(4, 5) = 1
* Legal ops: ~ &
* Max ops: 14
* Rating: 1
*/
int bitXor(int x, int y) {
int fx = ~x, fy = ~y;
int tx = fx & y, ty = fy & x;
return ~((~tx) & (~ty));
}tmin
这里的最小指的是补码对应数值最小...这个直接符号位填1就好了
/*
* tmin - return minimum two's complement integer
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 4
* Rating: 1
*/
int tmin(void) {
return (1 << 31);
}isTmax
tmax的特点是除了符号位都是1,那么加上1就得到了tmin,取反仍然是tmax
但是除了tmax还有别的数有这个性质:-1,排除掉就好了
//2
/*
* isTmax - returns 1 if x is the maximum, two's complement number,
* and 0 otherwise
* Legal ops: ! ~ & ^ | +
* Max ops: 10
* Rating: 1
*/
int isTmax(int x) {
int t = x + 1;
return !( ( (~t) ^ x) | (!t));
}allOddBits
lab有要求不能使用超过255的常量,那么一个想法就是把32bits分成4*8bits,
我们造一个(10101010)来复制4份就可以到奇数位全为1的二进制数,然后就很简单了
/*
* allOddBits - return 1 if all odd-numbered bits in word set to 1
* where bits are numbered from 0 (least significant) to 31 (most significant)
* Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 12
* Rating: 2
*/
int allOddBits(int x) {
int t = 170 | (170 << 8);
t = t | (t << 16);
return !((t & x) ^ t);
}negate
看trick4
/*
* negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
*/
int negate(int x) {
return (~x) + 1;
}isAsciiDigit
这道题就比较灵性...
观察一下asciiDigit的特点,最后6位都形如\((11xxxx)_2\),而最后4位恰好是\((0000)_2\sim (1001)_2\)
我最早的做法是把后6位抠出来,用倒数第4位判掉0~8的情况,再判掉最后2位的情况
事实上做了后面的isLessOrEqual就可以发现这里的另一种做法了...不是很懂这个顺序啊
//3
/*
* isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
*/
int isAsciiDigit(int x) {
int A = !( (x >> 4) ^ 3);
int B = !(x & 8);
int C = !(x & 6);
return A & ( B | C );
}conditional
利用trick3就可以做了,构造\(f(flag,x)\otimes f(!flag,y)\)就好了
我在写到这里的时候没有意识到trick4可以用,所以写的比较繁琐
/*
* conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
*/
int conditional(int x, int y, int z) {
int px1 = !x;
int px2 = !px1;
int ty = ( (px2 << 31) >> 31 ) & y;
int tz = ( (px1 << 31) >> 31 ) & z;
return ty ^ tz;
}isLessOrEqualTo
最直观就是做差,判断\(\triangle\)的符号位
然而当两个数异号的时候,他们的差会溢出,为了处理这种状况我们要先判掉异号的情况,这样同号运算就是在范围内的了
/*
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
int isLessOrEqual(int x, int y) {
int d = x + (1 + (~y) );
int fx = (x >> 31) & 1;
int fy = (y >> 31) & 1;
return ( (!d) | ( (d >> 31) & 1) | ( fx & (!fy) ) ) & !( (!fx) & fy);
}logicalNeg
可以发现符号位不重要,第一步先去掉符号位得到"绝对值"
如果是0的话取反就会得到-1,否则都得不到-1
此时加1又可以得到0,即符号位为正,而其余情况得到的都是负数
这个性质可以判掉"大部分"非0数字,特例是-2147483648,它没有绝对值(或者说,"绝对值"是0)...所以特判一下就好了
//4
/*
* logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
int logicalNeg(int x) {
int tx = (~x) | (1 << 31);
return ( ~( ( ( tx + 1 ) | x ) >> 31 ) ) & 1;
}howManyBits
先考虑正数,我们要找的就是最高位的1在哪(第几位)
负数的情况比较特殊,因为从符号位开始连续的1序列和单独的一个符号位1等价(回忆课堂上的Sign Extension),那么我们只需要保留一个符号位,也就是只需要找到最高位的0就可以了
于是负数就取反,找最高位的1可以用二分(魔幻吧),想了好久才想到...
先判断前16位是否有1,然后通过右移来调整下一次判断的区间,以此类推...就可以了
/* howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
int howManyBits(int x) {
int t1, L1, t2, L2, t3, L3, t4, L4, t5, L5;
int s = ~1 + 1, rx = x, cx = !x;
int p = (x >> 31) & 1, dx = !(rx ^ s);
x ^= ~p + 1;
t1 = s & (x >> 16); L1 = ( (!!t1) << 4); x >>= L1;
t2 = s & (x >> 8); L2 = ( (!!t2) << 3); x >>= L2;
t3 = (x >> 4) & s; L3 = ( (!!t3) << 2); x >>= L3;
t4 = (x >> 2) & s; L4 = ( (!!t4) << 1); x >>= L4;
t5 = (x >> 1) & s; L5 = (!!t5); x >>= L5;
return L1 + L2 + L3 + L4 + L5 + 2 + (1 + ~cx ) + (1 + ~dx);
}floatScale2
浮点数的编码很有意思
分类讨论。首先判掉NaN和INF,对于denorm的形式我们只要左移frac部分,对于norm形式我们只需要增加指数exp(why?)
这个例子大概是给你熟悉浮点数编码分类的
//float
/*
* floatScale2 - Return bit-level equivalent of expression 2*f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representation of
* single-precision floating point values.
* When argument is NaN, return argument
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatScale2(unsigned uf) {
unsigned s = (uf >> 31) & 1;
unsigned e = (uf >> 23) & 255;
unsigned m = uf & 8388607;
if (e == 0) {
m = m * 2;
} else if (e != 255) {
e = e + 1;
}
return (s << 31) | (e << 23) | m;
}floatFloat2Int
试了一下,C里面的强制类型转换会截掉小数点后的部分,除非某种类似1.9999999999999999999的例子,在这个例子下类型转换会变成2(why?)
事实上第二种情况我们不需要考虑,因此只需要把frac部分抠出来,前面添上1,按照exp-bias得到的指数位e偏移即可。很显然如果它是一个denorm/指数为负的norm的话答案就是0
/*
* floatFloat2Int - Return bit-level equivalent of expression (int) f
* for floating point argument f.
* Argument is passed as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point value.
* Anything out of range (including NaN and infinity) should return
* 0x80000000u.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
int floatFloat2Int(unsigned uf) {
int s = (uf >> 31) & 1;
int e = (uf >> 23) & 255;
int m = uf & 8388607;
int bias = 127, i = 22, r = 1;
if (e == 255) {
return 0x80000000u;
} else if (e == 0) {
return 0;
} else {
e -= bias;
if (e < 0) return 0;
for (; i >= 0; i --) {
if ( (m >> i) & 1) break;
}
while (e > 0) {
e -= 1; i -= 1; r <<= 1;
if (i > 0) r |= ( (m >> i) & 1);
if (r < 0) return 0x80000000u;
}
return s?(-r):r;
}
}floatPower2
这个也挺简单的...
从这个题可以看出单精度(32位)浮点数能表示的数字的范围
最大值是norm形式,exp为254(再大就是NaN和INF了),frac的每一位全为1(虽然在这题里不是这样),就能得到\({\left(2-\epsilon\right)}^{127}\)
最小值是denorm形式,exp为0,frac为1,此时指数e是1-127,尾数额外提供了23位的指数,这样就得到\(2^{-149}\)
这样直接做就可以了
/*
* floatPower2 - Return bit-level equivalent of the expression 2.0^x
* (2.0 raised to the power x) for any 32-bit integer x.
*
* The unsigned value that is returned should have the identical bit
* representation as the single-precision floating-point number 2.0^x.
* If the result is too small to be represented as a denorm, return
* 0. If too large, return +INF.
*
* Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatPower2(int x) {
int s = 0, m = 0, e = 127;
if (x < 0) {
if (-x > 149) return 0;
else if (-x <= 126) {
e = 1;
} else {
e = 0;
m = (0x400000u) >> (-x - 126);
}
} else if (x > 0) {
if (x + 127 > 255) return 0x7f800000;
else e = x + 127;
}
return (s << 31) | (e << 23) | m;
}