思考题的引入
首先看这样一道思考题:
如何用正则表达式识别所有是三的倍数的二进制串?
考虑最暴力的做法。用一个变量rem表示一个串的前缀作为二进制对3的余数,对新进来的字符讨论:
进来一个
0,则rem=(rem<<1)%3;,因为我们是从高位向低位读的进来一个
1,则rem=((rem<<1)+1)%3
那么只需要判断最终rem是否为0就好了
自动机的做法
在做这题之前,可以先想想这样的一个问题:
如何用自动机识别所有是三的倍数的二进制串?
或者说
如何用自动机表示上述暴力做法?
注意到rem的取值只能为0,1,2,因此可以建3个点,每个点两条出边表示对不同字符的处理转移,那么建出来的图如下
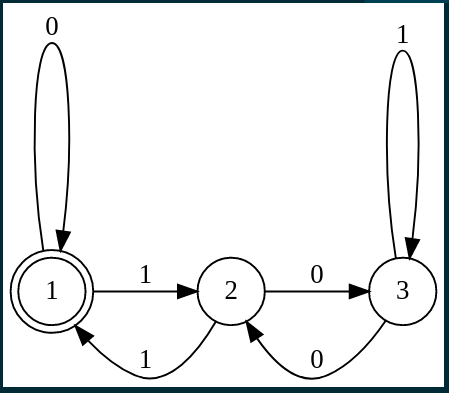
其中节点1,2,3分别表示rem对应为0,1,2的状态。
"但是问题还没完啊,你不是要正则表达式吗"
做到这一点需要一些前置姿势
正则表达式代数
没错!正则表达式也是有代数结构的!
为了方便,我们规定连接运算(concatenation)用.符号表示
它们的优先级从上到下递增
那么自然应该想到,列出正则表达式的代数方程,也是可以解方程的
Arden's Theorem
定理的内容很简单,即对于形如 \(x=A|xB\) 的方程,\(x\) 的解都是 \(AB^*\) 的形式
对解的长度进行归纳。当 \(n=1\), \(x_1=A\) 是原方程的一个解,满足 \(x=AB^*\) 的形式
设当 \(n<k\) 时成立,则 \(x_{n-1}=A\overbrace{B\ldots B}^{n-1\text{个}B}\),带入方程右侧就有 \(x_n=x_{n-1}B=A\overbrace{B\ldots B}^{n\text{个}B}\)
由数学归纳法可知原方程的解都是 \(x=AB^*\) 的形式,并且容易验证形如 \(AB^*\) 的串都是方程的解。
类似的也有对 \(x=A|Bx\) 的结论
自动机到正则表达式的转换
我们知道,自动机的每个状态都对应着一个接受串的集合(从初始状态到当前状态所有路径组成的串的并),而不同状态之间存在转移关系
那么就可以设未知数列方程辣!
对于最开始的那个DFA,我们可以设它的三个状态对应的接受串的正则表达式为\(x_0,x_1,x_2\),那么有如下关系
\[\begin{aligned} \begin{cases} x_0 &=& x_00|x_11 \\ x_1 &=& x_01|x_20 \\ x_2 &=& x_10|x_21 \\ \end{cases} \end{aligned}\]对式3用Arden's Theorem得到\(x_2=x_101^*\)
代入式2得到 \(x_1=x_01|x_101^*0=x_01(01^*0)^*\)
代入式1得到 \(x_0=x_00|x_01(01^*0)^*=x_0(0|1(01^*0)^*)=(0|1(01^*0)^*)^*\)
于是就得到了与该自动机等价的正则表达式
需要注意的是,在这个表达式中,我们认为可以有任意的前缀零,并且空串和任意长度的0串都是3的倍数
升华一下
如果你乐于思考,就会发现我们上述"消元"过程意味着什么——我们在化简自动机的状态!
也就是说,假如我们要求得表示DFA从起点到终点e的串的集合的正则表达式,那么我们只需要合并掉除起点和e以外的所有状态即可。